|
Lassen Sie sich den Artikel vorlesen:
|

- Das Gamma gibt die Veränderung des Deltas an, wenn sich der Preis des Basiswertes um eine Einheit verändert.
- Das Gamma ist bei Optionen am Geld am größten, da Preisänderungen des Basiswertes an dieser Stelle den größten Einfluss auf das Delta haben.
Gamma = Veränderung des Deltas bei einer Preisveränderung des Basiswertes
Die Funktion von Gamma
Die nebenstehende Tabelle zeigt das Delta und das Gamma von fünf Put-Optionen auf den DAX mit einer Laufzeit von 30 Tagen. Können Sie anhand des Delta und des Gamma eine Einschätzung abgeben, auf welchem Niveau der DAX-Index in diesem Beispiel steht?
Ein Delta von 0,5 bei Call-Optionen oder von -0,5 bei Put-Optionen zeigt an, dass eine Option am Geld ist. Die Put-Option mit einem Ausübungspreis von 9.900 kommt dem mit einem Delta von -0,48 am nächsten. Gleichzeitig ist das Gamma dieser Put-Option am größten, was bedeutet, dass sich der Ausübungspreis dieser Option offenbar in der Nähe des aktuellen DAX-Standes befindet. Der DAX-Index notierte in diesem Beispiel tatsächlich bei 9.892 Punkten.
| Ausübungspreis | Delta | Gamma |
| 9.700 | -0,38 | 0,00049 |
| 9.800 | -0,43 | 0,00051 |
| 9.900 | -0,48 | 0,00052 |
| 10.000 | -0,53 | 0,00051 |
| 10.100 | -0,58 | 0,00050 |
Wir erklären die Funktion von Gamma anhand eines Beispiels. Das Delta einer Put-Option auf den DAX-Index mit dem Ausübungspreis von 9.900 beträgt -0,48. Wenn der DAX von 9.892 auf 9.891 Punkte fällt, so verändert sich das Delta. Hierbei wird die Funktion des Gamma deutlich. Denn das Gamma gibt an, wie stark die theoretische Veränderung des Deltas ausfällt. Auf diese Weise lässt sich berechnen, wie hoch das Delta nach einer Kursveränderung um einem Punkt ist.
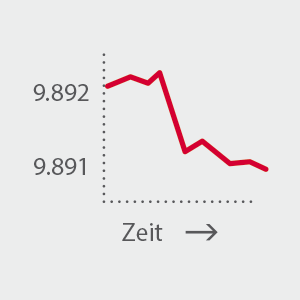

Ein Kursrückgang um einen Punkt sorgt dafür, dass sich das Delta der Put-Option 9.900 von -0,48444 auf -0,48494 verändert. Wenn der DAX-Index noch einen Punkt fällt (von 9.891 auf 9.890), dann ändert sich das Delta erneut. Es wird theoretisch um schätzungsweise 0,0005 höher liegen, bei etwa -0,48544. In der Praxis muss dies jedoch nicht exakt stimmen, da das Gamma genau wie das Delta nicht konstant ist, sondern lediglich ein Näherungswert für die tatsächliche angebots- und nachfragebedingte Preisbildung durch die Marktteilnehmer.
Eine Preisänderung im Basiswert wirkt sich auch auf die Höhe des Gammas aus. Wenn der DAX-Index von 9.891 auf 9.892 steigt, so sinkt das Delta für eine DAX Put-Option mit einem Ausübungspreis von 9.900 Punkten etwas. Der Kursanstieg um einen Punkt sorgt dafür, dass sich das Delta von -0,48494 auf -0,48444 verringert. Steigt der DAX um einen weiteren Punkt, so verringert sich das Delta auf ungefähr -0,48394.

Für einen Optionsanleger ist das Gamma aus folgendem Grund wichtig: Bei einer gekauften Option nimmt der Gewinn betragsmäßig zu, wenn die Kursbewegung des Basiswertes mit der gekauften Position übereinstimmt. Wenn Sie eine Call-Option besitzen und der Preis des Basiswertes steigt, so nimmt das Delta mit jedem zusätzlichen Punkt weiter zu. Die Zunahme des Delta sorgt dafür, dass der Preis der Call-Option in Geldeinheiten gerechnet stärker steigt. Der Gewinn des Optionsanlegers steigt also umso stärker, je weiter sich der Kurs des Basiswertes in die richtige Richtung entwickelt.
Andersherum nimmt der Verlust entsprechend ab. Die gekaufte Call-Option wird bei einem Absinken des Basiswertes mit dem ersten Punkt am meisten an Wert verlieren. Durch das Gamma wird das Delta umso kleiner, je weiter der Basiswert in den Verlustbereich fällt. Deshalb fallen die Verluste pro weiterem Punkt Kursrückgang beim DAX-Index betragsmäßig stets kleiner aus.
Dieses verlustbegrenzende Prinzip spricht Anleger natürlich an. Wenn Sie falsch liegen, dann werden die Verluste betragsmäßig immer kleiner, während der Gewinn bei einer richtigen Einschätzung des Marktes in Geldeinheiten gerechnet größer wird.
In der Realität gibt es jedoch noch weitere Einflussfaktoren, die bei der Preisbildung von Optionen eine Rolle spielen. Dem Gamma steht beispielsweise der Grieche Theta gegenüber, der den Verlauf der Zeit berücksichtigt.
Die Laufzeit bis zum Verfall
Die Laufzeit einer Option hat einen starken Einfluss auf das Gamma. Denn je kürzer die Zeit bis zum Verfall ist, desto heftiger sind die Schwankungen des Gamma. Eine Option am Geld hat bei einer Restlaufzeit von einer Woche ein größeres Gamma als bei einer Restlaufzeit von drei Monaten. Wie bereits erklärt, reagiert das Delta empfindlicher auf Veränderungen des Basiswerts, je näher das Verfallsdatum rückt. Dies hat zur Folge, dass auch das Gamma zum Verfallsdatum hin empfindlicher für Veränderungen wird.
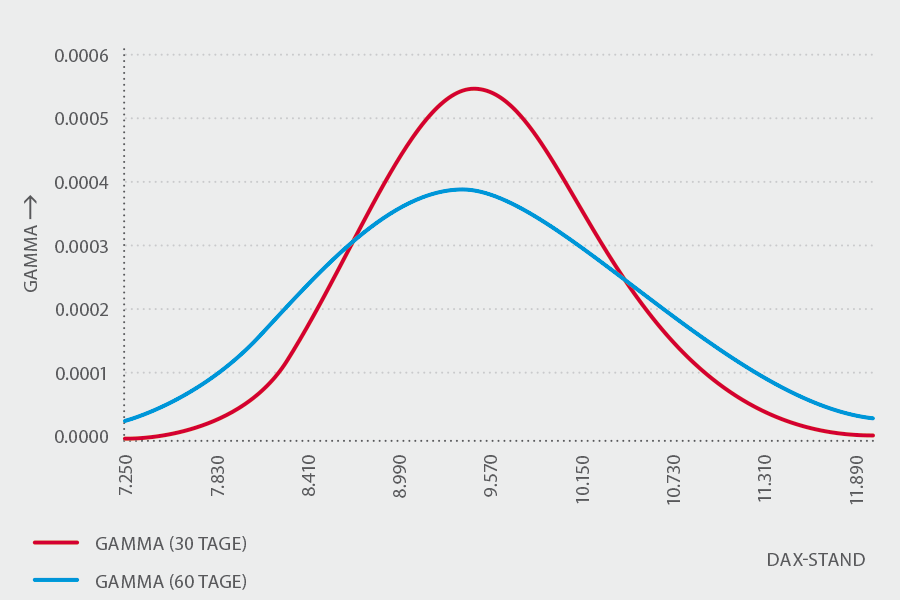
Die Abbildung zeigt das Gamma einer DAX-Index Call-Option 9.550. Die blaue Linie zeigt das Gamma bei 60 Tagen Restlaufzeit, während die rote Linie das Gamma bei 30 Tagen bis zum Verfall abbildet. Wenn das Verfallsdatum näher rückt, so fluktuiert das Gamma bei einer kürzer laufenden Option stärker als bei einer Option mit längerer Restlaufzeit. Die Abbildung zeigt, dass das Gamma bei einem DAX-Stand von 9.550, also wenn die Call-Option genau am Geld ist, jeweils den höchsten Wert hat. Je kürzer die Laufzeit der Option, desto größer ist das Gamma. Dies wird durch die rote Linie der 30-tägigen Call-Option sichtbar, die im Kursbereich um den Ausübungspreis herum über der blauen Linie der 60-tägigen Call-Option liegt.
Wir beabsichtigen nicht, diesen Artikel zu aktualisieren, aber wir könnten Analysen für dieselbe Aktie veröffentlichen.
Alles über Optionen:
Volatilität
Griechen